![]()
![]()
- Top Page
- Population & Household Projection
- Population Projections for Japan: 2016-2065
- Summary of the projection
![]()
Population Projections for Japan (2016-2065): Summary
- Population Size and Growth
- Population Age Composition
- Age Dependency Ratios
- Changes in the Population Pyramid
- Summary of the Results of Projections with the High-Mortality Assumption
- Summary of the Results of Projections with the Low-Mortality Assumption
- Jump-off Population
- Assumptions for Fertility Rates and Sex Ratio at Birth
- Assumptions for Survival Rates (Future Life Table)
- Assumptions for the International Migration Rate (Numbers)
- Long-range Auxiliary Projections and Conditional Projections
Based on the latest results from the Population Census of Japan and the Vital Statistics of Japan, the National Institute of Population and Social Security Research in Japan (IPSS) has conducted a new national population projection exercise (Population Projections for Japan). This is the 15th release of national population projections by the Institute, including the period before the integration of the Institute of Population Problems and the Social Development Research Institute.
I. Introduction
The Population Projections for Japan project the size and structure of the population into the future based on assumptions on future fertility, mortality, and international migration levels. Given that future changes in fertility, mortality, and international migration cannot be known with certainty, the IPSS projections provide a well-defined range of likely future population developments by computing variants based on alternative scenarios.
The projections cover the total population living in Japan, including non-Japanese residents. This is the same framework that is used by the Population Census of Japan. The period of the projections begins with the 2015 Population Census and continues until 2065, projecting the population as of October 1 for each year. Additionally, we extended the population calculations up to 2115 and added these as long-range auxiliary projections.
The method of projection is as follows: we set assumptions on individual components of population dynamics, i.e., birth, death, and international migration, by sex and age, and projected the population demographic trends by sex and age into the future using the cohort component method. Assumptions are made based on actual statistics for each component using the demographic method. (For further details, refer to section "III. Summary of the Method Used for Population Projections".)
II. Summary of Population Trends
The Population Projection for Japan is based on three alternative assumptions about future changes in both fertility and mortality (a low, medium, and high variant of each), resulting in a total of nine projections?one for each combination of these variants. Hereafter, the outline of the results of the three projections combining the three assumptions on fertility with the medium variant assumption for mortality will be presented first, followed by an outline of the results of the three assumptions of fertility combined with the high- and low-mortality assumptions. In the following descriptions, each projection is referred to by the combination of its respective fertility and mortality assumptions, e.g., medium-fertility (medium-mortality) projection.
A. The Results of Projections According to the Three Fertility Variants with the Medium-Mortality Assumption
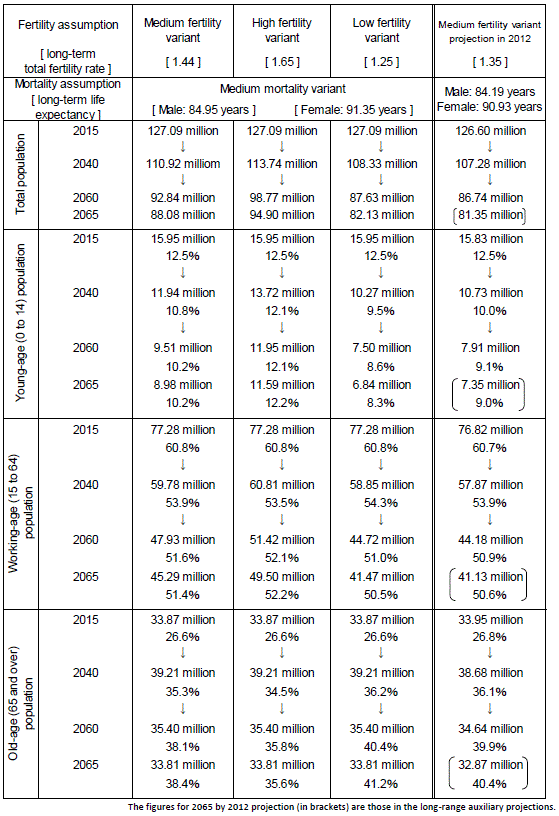
According to the 2015 Population Census, which serves as the base year for these projections, the total population of Japan in that year was 127.09 million (total population including non-Japanese residents).
Based on the results of the medium-fertility projection, Japan is expected to enter a long period of population decline. The population is expected to decrease to around 110.92 million by 2040, fall below 100 million to 99.24 million by 2053, and drop to 88.08 million by 2065 (see Table 1-1 and Figure 1-1).
Based on the results of the high-fertility projection, the total population is expected to drop below the 100 million mark to 99.52 million by 2059, and to decrease further to 94.90 million by 2065 (see Table 1-2 and Figure 1-1).
Conversely, based on the low-fertility projection, the total population is expected to fall below 100 million by 2049 and to decline to 82.13 million by 2065 (see Table 1-3 and Figure 1-1).
In comparison with the results for the previous projection (2065 by the long-range auxiliary projection), the total population increased by 6.72 million from 81.35 million to 88.08 million, and the year that the total population decreased to below 100 million was delayed by 5 years from 2048 to 2053 for the medium-fertility variant.
(1) Trends in the Young-age Population under 15 and its Share of the Population
The annual number of births in Japan (Japanese) has declined from 2.09 million in 1973 to 1.01 million in 2015. Consequently, the population of children under the age of 15 (young-age population) has also decreased from 27 million in the early 1980s to 15.95 million, as recorded in the 2015 Population Census.
According to the medium-fertility projection, the population size of this age group will fall to the 14 million mark by 2021 (see Table 1-1 and Figure 1-3). The decline will continue and the population of this age group is expected to fall below 10 million by 2056, eventually decreasing to around 8.98 million by 2065.
Looking at the different trends in the number of children in the high- and low-fertility projections, this age group is expected to be on the decline even in the high-fertility projection and will reach 11.59 million by 2065 (see Table 1-2). The low-fertility projection leads to a more rapid decline in the size of this age group; it is projected that this demographic group will shrink to below 10 million by 2044, and eventually decrease to as little as 6.84 million by 2065 (see Table 1-3).
Examining the declines of the young-age population in terms of the percentage of the total population, according to the medium-fertility projection, the share is expected to continue to shrink from 12.5% as of 2015 to 12.0% by 2020, drop to 11.0% by 2031, and eventually decrease to 10.2% by 2065 (see Table 1-1 and Figure 1-4).
The high-fertility projection shows a somewhat slower decline in the percentage of children, falling to 12.0% by 2041 and reaching 12.2% by 2065 (see Table 1-2).
The decline in the children's share of the population is of course rapid in the low-fertility projection, falling to 12.0% by 2019, falling below 10% by 2030, and ultimately dropping to 8.3% by 2065 (see Table 1-3).
(2) Trends in the Working-age Population (aged 15 to 64 years) and its Share of the Population
The population of the working-age group (from 15 to 64 years of age) increased consistently during the post-war years, reaching its peak at 87.26 million in the 1995 Population Census. However, since then, it has entered a period of decline and, according to the 2015 Population Census, the population has fallen to 77.28 million.
According to the results of the medium-fertility projection, the population of this age group is expected to continue to decrease to below 70 million by 2029, below 60 million by 2040, below 50 million by 2056, and will eventually drop to 45.29 million by 2065 (see Table 1-1 and Figure 1-3).
According to the projections based on the high- and low-fertility assumptions, until 2030, the working-age population trends exhibit the same overall behavior as those based on the medium-fertility assumptions. After 2030, the depopulation of this age group is expected to be slower in the high-fertility projection, not dropping below 50 million until 2064 and reaching 49.50 million by 2065 (see Table 1-2). According to the low-fertility projection, the working-age population is expected to decrease more rapidly, failing to below 50 million by 2051 and reaching 41.47 million by 2065 (see Table 1-3).
Looking at the proportion of the population in the working-age group, according to the medium-fertility projection, the proportion will continue to fall from its 2015 share of 60.8%, declining to below 60.0% by 2017, and eventually declining to 51.4% by 2065 (see Table 1-1 and Figure 1-4).
Similarly, in the high-fertility projection, the population share of the working-age group shows a constant decline from the start of the projection period, reaching 52.2% by 2065, just one percentage point higher than the result of the medium-fertility projection.
In the low-fertility projection, the proportion of this age group out of the overall population will be 50.5% by 2065, and about one percentage point lower than the projection based on the medium-fertility assumptions.
(3) Trends in the Old-age Population (65 years of age and over) and its Share of the Population
The trends exhibited by the old-age population (65 years of age and over) will be identical for all three fertility variant assumptions throughout the projection period of 50 years if the assumption of mortality is the same. That is, this age group will grow from 33.87 million as of 2015 to 36.19 million by 2020 (see Table 1-1, Table 1-2, Table 1-3, and Figure 1-3). It will then enter a period of modest increase for some time, reaching 37.16 million by 2030, and will peak by 2042, reaching to 39.35 million when the second baby-boom cohort enter this age group. The trend will subsequently shift to a steady decrease and the size of the age group will ultimately reach 33.81 million by 2065.
Looking at the proportion of the elderly out of the entire population, the share will increase from the current level of 26.6% as of 2015, meaning that more than one in four people in Japan will be elderly. By 2036, 33.3% of the total population, corresponding to one in three people, will be elderly, and 50 years after the start of projection period, in 2065, the elderly will account for no less than 38.4%, i.e., one in 2.6 people, according to the medium-fertility projection (see Table 1-1 and Figure 1-2).
The results of the high-fertility projections show that the share will be 33.6%, i.e., one in three people, by 2038 and 35.6% by 2065, i.e., one in 2.8 people in Japan will be elderly (see Table 1-2 and Figure 1-2).
In the low-fertility projections, the share will be 33.4% by 2035, i.e., one in three people, and 41.2% by 2065, i.e., one in 2.4 people in Japan will be elderly (see Table 1-3 and Figure 1-2).
A comparison of the results of the high- and low-fertility projections show that the variation in the aging trend, brought about by different assumptions of fertility rates, amounts to a difference of 1.7 percentage points by 2040, from 36.2% in the low-fertility projection to 34.5% in the high-fertility projection. Thereafter, this difference grows wider, resulting in a difference of 5.6 percentage points by 2065, where the low-fertility figure is 41.2% as opposed to the high-fertility figure of 35.6% (Figure 1-2).
As already noted, the elderly population will peak at 2042 and decrease thereafter. Nevertheless, according to both the medium- and low-fertility assumptions, the proportion of the elderly generation will continue to rise throughout the coming 50 years. This occurs because the child and working-age populations decrease faster throughout the period covered by the projections than the elderly age group.
In comparison with the results for the previous projection (2065 by the long-range auxiliary projection), the elderly population increased by 0.94 million from 32.87 million to 33.81 million and the share decreased by 2.0% points from 40.4% to 38.4% for the medium-fertility variant. The elderly population will peak by 2042. In the previous projection, the size of the elderly population is 38.78 million, whereas in the current projection the population size will be 39.35 million by 2042.
The (Total) age dependency ratio is an index that provides a rough indication of the level of support burden that is placed on the working-age group, through comparison of the relative size of the young-age population and old-age population groups with that of the working-age group. The old-age dependency ratio (the percentage of the old-age population relative to the population of the working-age group) based on the medium-fertility projection is projected to increase from 43.8 (an average of 2.3 workers supporting one senior resident) as of 2015 to 50.3 (two workers supporting one senior resident) by 2023, and eventually reaching 74.6 (only 1.3 workers supporting one senior resident) by 2065 (see Table 1-4). In contrast, the young-age dependency ratio (the percentage of the young-age population relative to the working-age population) was at the level of 20.6 (an average of 4.8 workers supporting one child) as of 2015, and will remain in the range of 19 to 21 in the future. Despite the decrease in the young-age population due to low fertility, the young-age dependency ratio is not expected to decrease below a certain level, because the working-age population will also simultaneously shrink in size.
The value obtained by adding the young-age dependency ratio and the old-age dependency ratio is referred to as the total age dependency ratio, and is used to indicate the degree of burden placed on the working-age population to support the entire young-age/old-age population. According to the medium fertility projection, under the shrinking working-age population, the total age dependency ratio is expected to increase from 64.5 as of 2015, to 80.5 by 2037, and will eventually reach 94.5 by 2065.
The age dependency ratio based on the high-fertility projection will initially follow a trend that is higher than that of the medium-fertility projection, because the young-age dependency ratio will be larger. However, the ratio of the high-fertility projection will show a decrease below that of the medium-fertility projection by 2047 and beyond, and is expected to reach 91.7 by 2065. Conversely, the age dependency ratio based on the low-fertility projection will initially maintain a lower level than that of the projections based on the medium-fertility projection, but the relationship will eventually reverse by 2047, and will reach 98.0 by 2065.
The population pyramid in Japan has significant irregularities due to acute fluctuations in past numbers of live births. For example, there was a decrease in the number of live births from 1945 to 1946 in line with the end of World War II, an increase known as the first baby boom from 1947 to 1949, a subsequent decrease from 1950 to 1957, and a sharp single-year drop in 1966 which corresponded to a period in the Chinese sexagenarian cycle that, owing to traditional beliefs, is accompanied by a sharp decline in birthrates. This was followed by a subsequent increase referred to as the second baby boom from 1971 to 1974, and a steady decrease thereafter (see Figure 1-5 (1)).
In the population pyramid as of 2015, members of the first baby-boomer generation are in their late 60s and those of the second baby-boomer generation are in their early 40s. Looking at the subsequent evolution of this pyramid shape according to the medium-fertility projection, the first baby-boomers will be in their early 90s and the second baby-boomers in their late 60s in 2040. It can therefore be concluded that the aging of society toward 2040 is characterized by the entry of the first and the second baby-boomer generations into the aged population (see Figure 1-5 (2)).
Thereafter, until 2065, the advancement of aging will reflect the fact that the population size of younger generations of all age brackets will decrease due to low fertility rates (see Figure 1-5 (3)).
B. The Results of Projections According to the Medium-Fertility Assumption with High- and Low-Mortality Assumptions
The high-mortality projection assumes higher mortality rates compared to the medium-mortality projection, which indicates slower advancements in mortality improvement and an overall life expectancy that remains at a relatively lower level. Therefore, under the same assumptions on fertility, the number of deaths will reach higher levels and the size of population will be remain at lower levels than in the medium-mortality projection throughout the projection period. That is, compared to the total population estimate of 88.08 million by 2065 based on the medium-fertility (medium-mortality) projection, the total population in the same year based on the medium-fertility (high-mortality) projection drops down to 86.40 million. Conversely, the population and demographics of the three major age groups based on the medium-fertility (high-mortality) projection are as follows: by 2065, the child population (and the proportion thereof) will be 8.97 million (10.4%), the working-age population (and the proportion thereof) will be 45.19 million (52.3%), and the elderly population (and the proportion thereof) will be 32.25 million (37.3%). These projections are lower than the results of the medium-fertility (medium-mortality) projection, and both the size and proportion of the elderly population, in particular, are smaller (see Table 2-1 and Table 3-4).
The low-mortality projection assumes a lower mortality rate than compared to the medium-mortality projection, which indicates faster advancements in mortality improvement and a life expectancy that remains at a relatively high level. In this case, the number of deaths will be relatively small and the population will maintain a higher level under the same fertility assumptions. That is, compared to the total population as of 2065 based on the medium-fertility (medium-mortality) projection, 88.08 million, the total population in the same year based on the medium-fertility (low-mortality) projection will be 89.74 million. On the other hand, the trends of the size and proportion of the three major age groups based on the medium-fertility (low-mortality) projection can be summed up as follows: by 2065, the child population (and the proportion thereof) will be 8.98 million (10.0%), the working-age population (and the proportion thereof) will be 45.38 million (50.6%), and the elderly population (and the proportion thereof) will be 35.37 million (39.4%). These results are higher than the results of the medium-fertility (medium-mortality) projection, and the size and proportion of the elderly population, in particular, is larger (see Table 2-2 and Table 3-4).
C. The Results of Projections According to the High- and Low-Fertility Assumptions with High- and Low-Mortality Assumptions (*)
In the Population Projections for Japan, we made four additional possible projections combining the high- and low-fertility assumptions and the high- and low-mortality assumptions in addition to the aforementioned projections. According to the high-fertility (low-mortality) projection, which results in the highest total population, the total population may potentially be as high as 96.57 million by 2065. Conversely, in the low-fertility (high-mortality) projection, which results in the lowest total population, the total population may be as low as 80.46 million in the same year (Table 3-1). Moreover, the proportion of the elderly population is 42.2% by 2065 according to the low-fertility (low-mortality) projection, which results in the highest proportion of the elderly population, while it is 34.6% in the same year according to the high fertility (high-mortality) projection, which results in the lowest proportion of the elderly population (Table 3-4).
* The tables showing the main results of these projections are not included in this report. Please refer to the Website of the National Institute of Population and Social Security Research in Japan for these tables.
III. Summary of the Method Used for Population Projections
As in the previous projections, the cohort component method is used for the Population Projections for Japan. This is a method of projecting the future population of each age- and sex-specific group according to assumptions about three components of population change, namely fertility, mortality, and migration.
Projecting the population using the cohort component method requires the following assumptions to be set for each sex and age group: (1) jump-off population, (2) future fertility rate (and the sex ratio at birth), (3) future survival rate, and (4) future international migration rates (numbers). In these projections, as in the past, we set these assumptions based on past trends for each component using the demographic method. Given that future changes in fertility and mortality cannot be known with certainty, we set multiple assumptions and produced multiple possible projections based on these assumptions, to provide a well-defined range of population projections.
For the jump-off population, which serves as the starting point of the projections, we used data on the total population by age and sex as of October 1, 2015. This was taken from the 2015 Population Census of Japan, which is compiled by the Statistics Bureau of the Ministry of Internal Affairs and Communications. This value was calculated by the Statistics Bureau of the Ministry of Internal Affairs and Communications as the jump-off population (as of October l, 2015) in the 2015 Population Census by evenly distributing the population of "not reported" nationality and age included in the 2015 Population Census (the results of a basic complete tabulation on population and households) in order to project the future population based on the population obtained in the Population Census.
Projecting the future number of births in the projections requires data on the female age-specific fertility rate of the year in question. In the present projections, we used cohort fertility data to estimate the future fertility rate. In this method, we observe the birth process per female birth cohort (a population group born in the same year) over the course of their lives, and forecast the fertility rate for cohorts whose birth process is incomplete for each year until the process is complete. The future age-specific and total fertility rates on an annual basis can be obtained by converting the cohort age-specific data into annual data. Note that we analyzed the past records of births from Japanese women only, based on which we projected the fertility trend for the whole population base with the aim of obtaining further precision in the determination of fertility rate trends. Therefore, the assumed index figures in relation to marriage and childbirth described hereafter all refer to Japanese women (the approach to handling the fertility rate of non-Japanese women is explained later).
Cohort age-specific fertility rates were statistically estimated and/or assumptions were set by birth order by way of models that use the lifetime probability of birth, age of childbearing, and so forth. That is, in the case of cohorts that are currently going through the birth process, the lifetime birth process is statistically estimated from the actual figures derived during the birth process. For young cohorts for whom only scant or no actual birth data is available yet, the index at the completion of the birth process was calculated based on indexes projected separately for the reference cohort. Note that the reference cohort refers to women born in 2000. We projected individual index values for first marriage behavior, couples' reproductive behavior, and behavior pertaining to divorce, bereavement, and remarriage based on actual statistics, and set the total cohort fertility rate and the distribution by birth order based on the calculation results for those index values.
The trends in individual index values for the reference cohort are as follows. With regard to first marriage behavior, the mean age at first marriage for women has been increasing and will likely continue to increase. As for the proportion of women who have never been married at 50 years of age, which expresses the effect for unmarried women, we observed the increase of the proportion because of the rise in age of marriage (due to postponement of marriage) as well as the fact that more women avoid marriage. The proportion of never married women at 50 years of age according to the medium-fertility variant, which is considered as a standard assumption, is projected to increase from the recently completed cohort, although the level is considered to be slightly lower than that of the reference cohort in the 2012 projection.
The completed number of births from married couples, which is an indicator for couples' reproductive behavior, is affected by the structural change caused by delayed marriage and childbearing, and by the changes in the reproductive behavior of couples. The expected completed number of births from married couples showing the structural effect for delayed marriage and childbearing is projected to decrease at a higher pace than before as a result of the increase in the mean age at first marriage. The index indicating changes in the reproductive behavior of couples (fertility variation coefficient of married couples) decreases remarkably for the cohort born in the 1960s, whereas the decline in the reproductive behavior of couples is mitigated for the cohort born after the 1970s by the births after 30 years of age. Therefore, the completed number of births from married couples in the medium-fertility variant is projected to reach a higher level than that of the reference cohort in the 2012 projection, although the level is lower than that of the actual recent cohort.
We can obtain the effects of divorce, bereavement, and remarriage on fertility rates (the coefficient of divorce, bereavement, and remarriage) as a coefficient of the completed number of births from women with these experiences and the trend of structural changes in marital status, divided by the fertility level of first-marriage couples who have completed the birth process. This coefficient is considered to be a higher level than that of the reference cohort in the 2012 projection, since the divorce rates have recently remained at almost the same level and the diminishment of the fertility level by divorce, bereavement, and remarriage is thereby mitigated.
Because the future development of fertility is uncertain, we decided to set the aforementioned three assumptions (medium-, high-, and low-variant projections) and project the future population based on each assumption. This approach accounts for a certain range of fluctuation that can be expected in the future population trends brought about by changes in birth view from the current state.
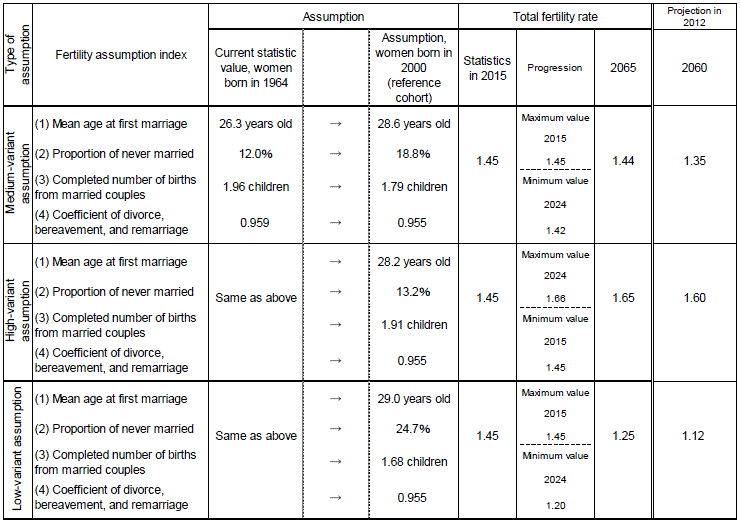
(1) Medium-fertility Assumption
(i) (i) The mean age at first marriage of women by cohort increases gradually from 26.3 years of age for the cohort born in 1964, to 28.6 years of age for the cohort born in 2000. It levels off at nearly the same level until the cohort born in 2015, and remains unchanged thereafter.
(ii) The proportion of women who have never been married at 50 years of age increases from 12.0% for the cohort born in 1964, to 18.8% for the cohort born in 2000. It then levels off at nearly the same level until the cohort born in 2015, and remains unchanged thereafter. .
(iii) Delayed marriage, delayed childbearing, and changes in the reproductive behavior of couples affect the completed number of births from married couples. Using couples with wives in the cohorts born between 1935 and 1954 as a benchmark (1.0), the index indicating changes in the reproductive behavior of couples (fertility variation coefficient of married couples) declines to 0.957 children for the cohort born in 2000. It remains at nearly the same level until the cohort born in 2015, and remains unchanged thereafter. The completed number of births from married couples is obtained from this index and the change in first marriage behavior as outlined in assumptions (i) and (ii) above, and drops from 1.93 for the cohort born between 1963 and 1967 to 1.79 for the cohort born in 2000, remaining unchanged thereafter.
(iv) We obtained the effects of divorce, bereavement, and remarriage on fertility rates (the coefficient of divorce, bereavement, and remarriage) based on the completed number of births from women with these experiences and the trend of structural changes in marital status. As a result, by setting the fertility level of first-marriage couples who have completed the birth process as a benchmark (l.0), the coefficient of divorce, bereavement, and remarriage decreases from the actual figure of 0.959 for the cohort born in 1964, to 0.955 for the cohort born in 2000 and maintains almost the same levels up to the cohort born in 2015. It remains unchanged thereafter.
As a result of assumptions (i) to (iv) above, the total cohort fertility rate of Japanese women decreases from the actually observed figure of 1.630 for the cohort born in 1964 to 1.397 for the cohort born in 2000. It remains almost constant until the cohort born in 2010, and remains unchanged thereafter.
We converted the cohort age-specific fertility rates obtained above into an annual fertility rate. Subsequently, we assumed that the relationship between moments of the fertility rate of non-Japanese women obtained from the actual statistics and that of Japanese women to be constant, and used it as a basis to obtain the age-specific fertility rate of non-Japanese women. With this operation, it becomes possible to calculate the fertility rate with the same definition as the Vital Statistics (i.e., the fertility rate including children of Japanese nationality born from women of non-Japanese nationality; see the formula below).

* A child with Japanese nationality born from a non-Japanese female is a child whose father is Japanese.
The results of the calculations above show that the total fertility rate of the same definition as the Vital Statistics, whose statistic value was 1.45 in 2015, is expected to gradually drop until it reaches 1.42 by 2024, whereupon it will increase slightly to 1.43 by 2035 and 1.44 by 2065 (see Table 4-1 and Figure 4-1).
With regard to the comparison of the total fertility with the previous projection at the end of the projection periods, the rate increased from 1.35 (2060) to 1.44 (2065) due to the improvement in the actual fertility rates for women in their 30s and 40s in recent years.
(2) High-fertility Assumption
(i) The mean age at first marriage of women by cohort will advance to 28.2 years of age for the cohort born in 2000, reach 28.1 years for the cohort born in 2015, and remain unchanged thereafter.
(ii) The proportion of women who have never been married at 50 years of age increases to 13.2% for the cohort born in 2000, ultimately dropping to 13.1% for the cohort born in 2015, and remains unchanged thereafter.
(iii) Using couples with wives in the cohorts born between 1935 and 1954 as a benchmark (1.0), the fertility variation coefficient of married couples, which indicates changes in the reproductive behavior of couples, declines temporarily but returns to 1.0 before the cohort born in 2000. The completed number of births from married couples derived from this coefficient and changes in first marriage behavior explained above will reach 1.91 children for the cohort born in 2000, maintain almost the same level up to the cohort born in 2015, and it will remain unchanged thereafter.
(iv) The coefficient of divorce, bereavement, and remarriage will decrease from the actual figure of 0.959 for the cohort born in 1964 to 0.955 for the cohort born in 2000, and maintain almost the same levels up to the cohort born in 2015, remaining unchanged thereafter.
From the assumptions (i) to (iv) above, the total cohort fertility rate of Japanese women is projected to decrease from the actual figure of 1.630 for the cohort born in 1964 to 1.591 for the cohort born in 2000, eventually reaching 1.594 for the cohort born in 2015 and remains unchanged thereafter.
Total fertility rate with the same definition as the Vital Statistics will, under the above assumptions, increase from the actual figure of 1.45 as of 2015 to 1.66 by 2024, eventually dropping to 1.65 by 2065 (see Table 4-1 and Figure 4-1).
(3) Low fertility Assumption
(i) The mean age at first marriage of women by cohort will increase to 29.0 years of age for the cohort born in 2000, and to 29.1 years of age for the cohort born in 2015 and remains unchanged thereafter.
(ii) The proportion of women who have never been married at 50 years of age increases to 24.7% for the cohort born in 2000, and maintains almost the same level up to the cohort born in 2015, remaining unchanged thereafter.
(iii) Uing couples with wives in the cohorts born between 1935 and 1954 as a benchmark (1.0), the fertility variation coefficient of married couples, which indicates changes in the reproductive behavior of couples, declines steadily to 0.909 for the cohort born in 2000, eventually reaching 0.910 for the cohort born in 2015 and remains unchanged thereafter. The completed number of births from married couples derived from this coefficient and the changes in first marriage behavior described above will decrease to 1.68 children for the cohort born in 2000, and remain unchanged until the cohort born in 2015 and thereafter.
(iv) The coefficient of divorce, bereavement, and remarriage will decrease from the actual figure of 0.959 for the cohort born in 1964, to 0.955 for the cohort born in 2000, and maintain almost the same levels up to the cohort born in 2015, remaining unchanged thereafter.
Based on assumptions (i) to (iv) above, the total cohort fertility rate of Japanese women will decrease from the actual figure of 1.630 for the cohort born in 1964, to 1.213 for the cohort born in 2000, eventually reaching 1.210 for the cohort born in 2015 and remains unchanged thereafter.
The total fertility rate with the same definition as the Vital Statistics will, under the above assumptions, decrease from the actual figure of 1.45 as of 2015 to 1.20 by 2024; thereafter, it will exhibit a slight increase to 1.25 by 2065 (see Table 4-1 and Figure 4-1).
Regarding the sex ratio at birth (the number of male children for every 100 female children) that is used to divide the future number of newborns into male and female births, we assumed the actual figure for the five years from 2011 to 2015 (105.2) to remain constant for 2016 and thereafter.
In order to project the population from one year to the next, survival rates by age and sex are needed, and in order to obtain future survival rates, it is necessary to construct future life tables. In the Projections, we have adopted the Lee-Carter model, which is currently internationally recognized as the standard model, to construct future life tables. We modified the model by adding new features so that the model adapts properly to Japan's characteristic mortality trend, which exhibits the highest level of life expectancy in the world. The Lee-Carter model describes the change in mortality rates for each age according to the change in the general mortality level by decomposing the matrix of age-specific mortality rates into a standard age schedule, a general level of mortality (mortality index), age-specific mortality rate changes relative to the mortality index, and an error term. In the Projections, we used the Lee-Carter model for the younger generations and combined it with a model that expresses the mortality rate improvement as a shift of the mortality rate curve to the advanced age side (linear differential model) for the older generations, in order to adapt to the mortality conditions of Japan, where mortality' rate improvement is notable. Note that the linear differential model describes the difference in the shift of the elderly mortality rate curve in the horizontal direction by a linear function of age.
When projecting the future mortality index, we used data from after 1970 in order to reflect changes in the level of mortality that gradually slowed down in recent years. From the perspective of ensuring consistency in terms of the mortality rate of men and women, curve fittings were applied simultaneously for both men and women. For the amount of shift and the gradient of the mortality rate curve to the advanced age side used in the linear differential model, we used the rate of change of the mortality index to make projections.
Because the improvement in Japanese mortality levels in recent years is showing trends beyond the assumptions of existing theories, we judged that the future mortality rate transitions and achieved levels will be highly uncertain as in the previous projections. Therefore, in the projections we decided to create multiple assumptions to obtain a likely fluctuation range for the projections. That is, we obtained the distribution of mortality index parameters for the standard mortality rate trend via the bootstrap method, and similarly used the distribution to estimate the 99% prediction interval of the mortality indices. Additionally, we added a "high-mortality" assumption with a high mortality rate, in which the mortality index remains at the upper limit level of the confidence interval, and a "low-mortality" assumption with a low mortality rate, in which the mortality index remains at the lower limit of the confidence interval.
Based upon the parameters and variables obtained through the procedures above, we finally calculated age- and sex-specific mortality rates until 2065 to construct the future life tables.
(1) Medium-mortality Assumption
According to the standard future life tables, life expectancy, which was 80.75 years for men and 86.98 years for women in 2015, is expected to grow to 83.27 years for men and 89.63 years for women by 2040, and 84.95 years for men and 91.35 years for women by 2065 (see Table 4-2 and Figure 4-2).
(2) High-mortality Assumption
According to the high-mortality assumption, the mortality rate will be higher and life expectancy will be shorter than compared to the medium variant. As a result, life expectancy according to this assumption will be 82.38 years for men and 88.71 years for women by 2040, and 83.83 years for men and 90.21 years for women by 2065.
(3) Low-mortality Assumption
According to the low-mortality assumption, the mortality rate will be lower and life expectancy will be longer than compared to the medium variant. As a result, life expectancy according to this assumption will be 84.15 years for men and 90.54 years for women by 2040, and 86.05 years for men and 92.48 years for women by 2065.
The trend of international migration is significantly influenced by the advancement of globalization and changes in socio-economic conditions, as well as the policies and regulations concerning international migration. In addition, socio-economic events and the occurrence of disasters inside and outside Japan can also bring about great fluctuations in international migration. Recent examples of such incidents include the terrorist attacks in the United States in 2001, the outbreak of SARS (Severe Acute Respiratory Syndrome) between 2002 and 2003, and the Lehman Crisis in 2008. Most recently, the Great East Japan Earthquake in March of 2011 had a significant impact on the immigration and emigration of non-Japanese people into and out of Japan.
The actual figures show that the trends of international migration rates and numbers differ between Japanese and non-Japanese populations. Additionally, considering the demographics, the movement of the Japanese population is influenced by the age structure of the population; however, for the non-Japanese population, the relation of their movement to the population size or age structure of Japan is limited. Therefore, in the projections, we made separate assumptions on international migration for the Japanese and non-Japanese populations. We set the figures of the Japanese population based on the net international migration rate, and those of the non-Japanese population based on the number of net migrants.
Looking at the actual statistics of international migration, the Japanese population shows a tendency of exits exceeding entries. In addition, the age patterns of the net international migration rate (net migration rate) by sex are relatively stable. We thus obtained the average value of the age- and sex-specific annual net international migration rate of Japanese people between 2010 and 2015 (using values for 4 years, excluding the maximum and minimum values for each age), smoothed out the rates to remove random fluctuations, and set the result as the net international migration rate of Japanese people for 2016 and onward (Table 4-3 and Figure 4-3).
Looking at the actual statistics of international migration of the non-Japanese population, the number of net migrants has generally shown a continuous increase, although some irregular fluctuations have been observed. However, quite recently, a large-scale excess of exits was observed due to the Lehman Crisis and the Great East Japan Earthquake. The trends of immigration and emigration of non-Japanese people showed great fluctuations in a short period of time. For this reason, we deliberately excluded data from years considered to show significant temporary transitions due to socio-economic events, disasters, etc. from our estimation of the number of net migrants of non-Japanese origin since 1970, projected a long-term trend of the number of net migrants, and set the result as the assumption until 2035. Note that the sex-specific number of net migrants of each year was calculated using the average values of the sex ratio of the number of net migrants from 1970 onward, and the age-specific proportion was obtained by smoothing the average values from 1986 to 2015, for which actual statistics are available (Table 4-4 to 4-5, Figure 4-4 to 4-5). However, in the long run, the scale of international migration of non-Japanese people must be interlocked with the population scale of Japan. We therefore obtained the age- and sex-specific net international migration rate in 2035 in each projection (using the total population of Japanese and non-Japanese people as the denominator) and assumed it to be constant thereafter.
* In this paper, we call the nine projections made by the above method until 2065 as "the basic projections."
(1) Long-range Auxiliary Projections
Although the end of the projection period for the basic projections is 2065, we made long-range auxiliary projections for the period from 2066 to 2115, which may be used as a reference for analysis of long-term population projections. In these projections, the survival rate-fertility rate, sex ratio at birth, and international migration rate are assumed to remain constant from 2066 (Table 5-1 to 5-6).
(2) Conditional Projections
Conditional projections are quantitative simulations for analyzing the responses of future populations to the changes of the assumptions in mechanical manners, which are made by means of basic projections every time to understand the results more clearly. In this paper, the results of the counterfactual simulations of the future population corresponding to various scenarios with different fertility and non-Japanese net migration levels are exhibited.
For the fertility rate, we use the three assumptions in the basic projections and create age-specific fertility rates by linear interpolation (extrapolation) of age-specific fertility rates for the three assumptions. As for the levels, we set the total fertility rates with the same definition as the Vital Statistics in 2065 as 1.00, 1.20, 1.40, 1.60, 1.80, 2.00, and 2.20.
For the non-Japanese net migration, we use the assumptions in the basic projections and create the number of net migrations for each year until 2035 by multiplying a single coefficient to those in the basic projections. As for the levels, we set the number of net migration in 2035 as 0, 50 thousand, 100 thousand, 250 thousand, 500 thousand, 750 thousand, and 1 million. As in the basic projections, we obtained the age- and sex-specific net international migration rate in 2035 in each projection (using the total population of Japanese and non-Japanese people as the denominator) and assumed it to be constant thereafter.
As for the results of the conditional projections, trends in total population and the proportion of the old-age population out of the entire population are exhibited in comparative tables.
* In the basic projections, neutrality and objectivity of the results are ensured by setting assumptions for fertility, mortality, and international migration using demographic projection methods based on the latest actual data as shown in the "Summary of the Method Used for Population Projections." Population projections could only become a common basis for planning in various areas through this procedure. (In light of the methodology in the setting of assumptions, the basic projections appear to show population trends in the change of the current society that would continue in the future).
IV. Summary Tables and Figures
A. Summary of Results and Assumptions
Summary of Projection Results (medium mortality variant projection)
Summary of the Method used for Projections
We set assumptions on individual components of the population dynamics, i.e., birth, death, and international migration and projected the future population using the cohort component method. Assumptions are made based on the past demographic dynamics for each component using the demographic method.
(1) Summary of Fertility Assumptions
We set assumptions on marriage and fertility indexes of the female cohort born in 2000 (reference cohort) and assumed that the fertility will develop from the empirical values or estimated values of older cohorts to that of the cohort born in 2015, and will remain constant thereafter.
Sex ratio at birth: The average value of the sex ratio at birth (105.2) from 2011 to 2015 is assumed to remain constant thereafter.
(2) Summary of Mortality AssumptionsWe made the "medium-mortality" assumption (84.95 years for men and 91.35 years for women by 2065) based on the statistics of mortality from 1970 to 2015, and set the "high-mortality" assumption (83.22 years and 89.96 years for men and women, respectively) and the "low-mortality" assumption (85.14 years and 91.90 years for men and women, respectively) according to the 99% confidence interval of the mortality index parameters.

For Japanese migration, we assumed that the average of the sex- and age-specific net international migration rate (net migration rate) from 2010 to 2015 would remain constant thereafter. For non-Japanese migration, we projected the trend of the number of net migrants in 1970 and onward, and used this trend as the assumption. The number of net non-Japanese migrants is expected to reach 33,894 men and 35,380 women by 2035. In subsequent years, the sex- and age-specific net international migration rate of non-Japanese people was set to be constant (using the total population as the denominator).