４． 生残率の仮定（将来生命表）

(3) 将来生命表の推計方法

　今回の推計では、現在国際的に標準的な方法とされるリー・カーター・モデルを採用しつつ、これに対して世界の最高水準の平均寿命を示すわが国の死亡動向の特徴に適合させるため、新たな機構を加えて用いた。すなわち、若年層ではリー・カーター・モデルを用いつつ、高齢層では、死亡率改善を死亡率曲線の高齢側へのシフトとして表現するモデル（線形差分モデル）を組みあわせることにより、死亡率改善のめざましいわが国の死亡状況に適合させた。

なお、線形差分モデルとは、高齢死亡率曲線の横方向へのシフトの差分を年齢の線形関数によって記述するモデルであり、

τ_y,t＝f^'_t＋g^'_tx

で表される。ただし、τ_y,tは年次( t )、対数死亡率（ y )の年齢シフト（差分）、f^'_t,St g^'_tx はそれぞれ差分を線形関数で表したときの切片と傾きを表す。ただし、実際のパラメータ推定は、この式を変形して対数死亡率の逆関数を

ν_y,t＝f_t＋g_tx＋a_y

と表し、さらに将来推計にあたっては、まず、死亡率曲線全体のシフト量S_tを測定し³¹⁾、S_tとg_tからf_tを求めた。また、今回の推計では、リー・カーター・モデルに線形差分モデルを組み込む観点から、対数死亡率曲面上の接ベクトル場の概念を利用し、「各時点・各年齢での死亡率改善方向の特定」をモデリングの基礎として、死亡率曲線の自由な方向（縦横を含む）への変化を統一的に扱う数理モデルを用いている。

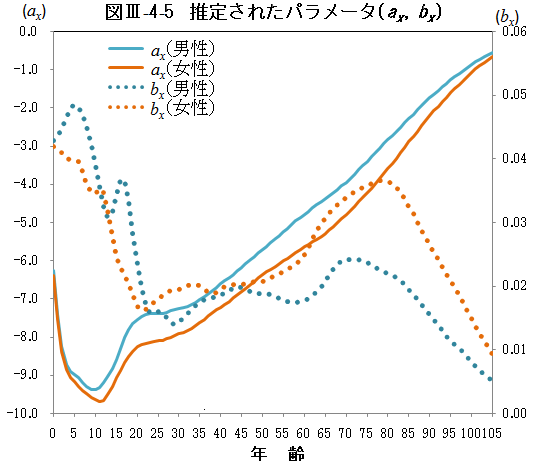
　推計の基礎とするデータは昭和45(1970)〜平成22(2010)年の死亡率m_x,tとし³²⁾、これにリー・カーター・モデルを適用するため、a_xとして直近5年間の平均値を取り、行列　ln(m_x,t)−a_xに特異値分解を施して、第一特異値に対応する項に基づきパラメータk_t,b_xを推定した³³⁾
(図�V-4-5, 図�V-4-6)。




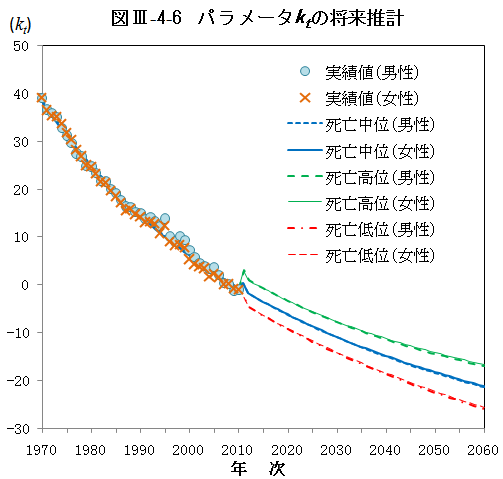
　死亡指数k_tの将来推計にあたっては、近年、徐々に緩やかになっている死亡水準の変化を反映させるために、関数あてはめを行って補外することにより推計を行った。

推計のための関数としては、平成14年推計から用いられている関数（指数関数と対数関数の平均³⁴⁾）が我が国の死亡指数の推移をよく表現しているとの観察に基づき同じ関数を用いた。

また、男女の死亡率をより整合的に推計する観点から、男女の死亡指数を組み合わせた行列に特異値分解を行い、第一特異値に対応する項の時系列変化に対して関数あてはめを行った後、男女別の死亡指数を推計した。なお、近年の死亡水準の改善が従来の理論の想定を超えた動向を示しつつあることから、今後の死亡率推移ならびに到達水準については不確実性が高いものと判断し、複数の仮定を与えることによって一定の幅による推計を行うものとした。

すなわち、標準となる死亡率推移の死亡指数パラメータの分散をブートストラップ法等により求め、これを用いて死亡指数が確率99%で存在する区間を推定し、死亡指数k_tがその上限を推移する高死亡率推計である「死亡高位」仮定、下限を推移する低死亡率推計である「死亡低位」仮定を付加した³⁵⁾(図�V-4-6)。



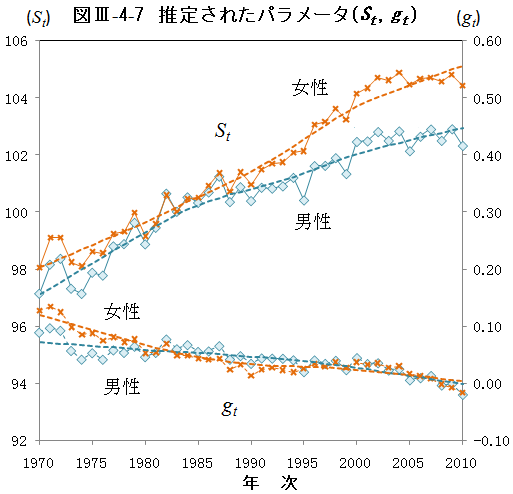
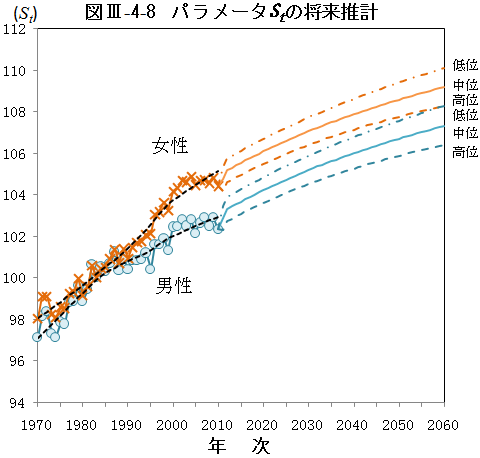
　また、線形差分モデルに関するパラメータS_tとg_tの推定結果を示したものが図�V-4-7である。将来推計にあたり、S_tについては過去15年間の死亡指数に対する変化率を用いて将来推計し、g_tについては直近の平均値（過去5年分）を将来に向けて固定した ³⁶⁾ (図�V-4-8)。

以上の手続きにより求められたパラメータと変数から最終的に平成72（2060）年までの死亡率を男女別各歳別で算出し、将来生命表を推計した。

なお、平成23(2011)年については東日本大震災が発生したことから、人口動態統計の死亡数、及び警察庁、岩手・宮城・福島県警察による被害状況データを用い、震災の影響を織り込んだ生命表を別途算定して仮定した。





(4) 将来生命表の推計結果

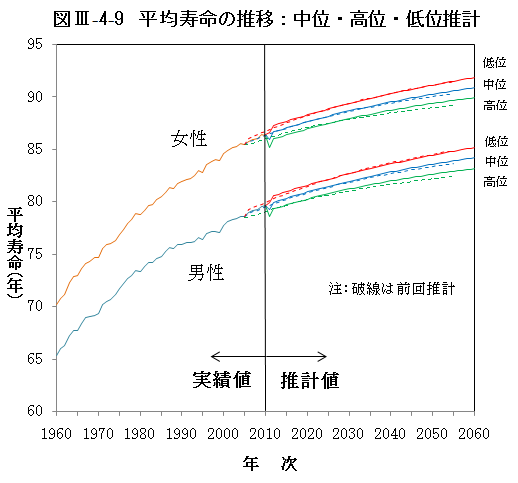
　将来生命表に基づく男女別平均寿命の推移を図�V-4-9に示した。

(1) 死亡中位の仮定について
　標準的な将来生命表に基づくと、平成22(2010)年に男性79.64年、女性86.39年であった平均寿命は、平成32(2020)年に男性80.93年、女性87.65年、平成42(2030)年に男性81.95年、女性88.68年となり、平成72(2060)年には男性84.19年、女性90.93年となる。

(2) 死亡高位の仮定について
　死亡高位の仮定では、中位仮定に比べて死亡率が高めに、したがって平均寿命は低めに推移する。その結果、この仮定においては、平均寿命は平成42(2030)年に男性81.25年、女性87.97年となり、平成72(2060)年には男性83.22年、女性89.96年となる。

(3) 死亡低位の仮定について
　死亡低位の仮定では、中位仮定に比べて死亡率が低めに、したがって平均寿命は高めに推移する。その結果、この仮定においては、平均寿命は平成42(2030)年に男性82.65年、女性89.39年となり、平成72(2060)年には男性85.14年、女性91.90年となる。



31) 死亡率の値が0.5(2パラメータロジスティック曲線の変曲点)となる点を用いて測定する。

32) 本推計では、国立社会保障・人口問題研究所「わが国の長寿化の要因と社会・経済に与える影響に関する人口学的研究」プロジェクトにおいて作成された「日本版死亡データベース」を基礎データとして用いている。

33) 実行列Xは、二つの直交行列U,Vと対角要素以外が0である行列Sを用いてX＝USVTと表すことができるが、これをXの特異値分解と呼び、このときのSの0でない要素を特異値と呼ぶ。これによって死亡水準の相対的変化を表す行列 ln(m_x,t)−a_xを、年齢・年次変化にともなう有効度に応じた幾つかの成分に分解することができる。

34) 指数関数はk_t＝α₁exp(α₂t)＋α₃、対数関数はk_t＝β₁ln(t＋β₂)＋β₃として当てはめた。ここでtは時間、α_nとβ_nは定数である。



36) Bongaarts, J (2005), “Long-range Trends in Adult Mortality: Models and Projection Methods”, Demography, 42, pp.23-49.では、各国のデータから勾配 が時系列的に概ね一定であるとの観察に基づき、死亡率曲線をロジスティック曲線に年齢シフトを組み合わせたshifting logistic modelというモデルで表すことを提案している。

---

第�V章目次へ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　前へ次へ